• References (links below)
• Ext. circuit is the Stator
• Bilateral symmetry version
• Pipecaps and mercury
• Shorted-load configurations
• Untested o/u heater
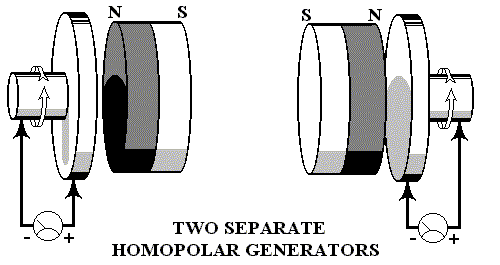
• Two separate n-machines
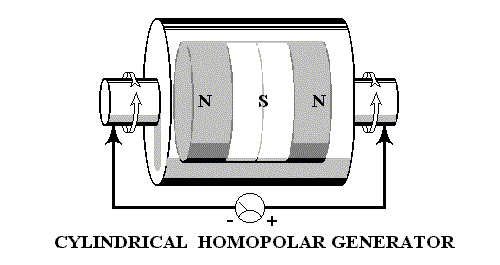
• Two n-machines merged (cylinder version)
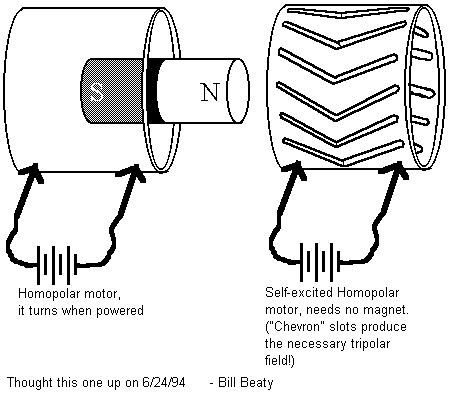
• Untested self-excited cylindrical motor
• E-fields around a rotating disk magnet?

• Homopolar motor and more youtube
• Links:
  • "N-machine"
  • BUY THIS BOOK:
    The Homopolar Handbook
  • INSTEAD OF MERCURY:
    try liquid Galinstan or buy Gallium

The general idea was that an HPG might lack back-torque if the rotor and stator circuits are radially symmetrical. If all wires were replaced with cups and tubes, would the mechanical energy per output wattage be reduced? If this were true, conservation of energy would be violated. The generator would create large currents and heat output, yet it would require little driving energy. If a pair of these was hooked together in motor/generator configuration, they might self-accelerate anomalously and spin without extrnal energy input. Impossible by standard physics, of course. Yet a radially-symmetric HPG does not change flux linkage when rotating, and so it might not be expected to produce output currents. Yet it does. Tewari and Depalma in fringe-science publications claim to have observed anomalous behavior when investigating these devices. If there is a way to extract the energy of the quantum vacuum sea, perhaps here is a device which accomplishes the feat.

The pipecaps/mercury experiment was my crude attempt to detect changes in electromagnetic braking in a shorted, symmetrical HPG. I hoped to compare the braking forces with and without the permanent magnet present. Unfortunately my setup didn't show low friction without the magnet, since the oxide crust on the mercury contributed a large friction compared to the EM braking effects. The crust/scum on the mercury gave such high friction that I couldn't see any obvious difference between the magnet version and the no-magnet version. To detect forces, I only relied on twisting up the thread and making crude time measurements of the unwinding. Later I realized that the crust could be eliminated. This experiment needs to be repeated.

In thinking long and hard about HPGs, I have come up with some observations and questions. Are you confused about spinning magnets versus spinning disks? Here's more to think about. Perhaps it will help to clarify things.

The diagram below depicts a simplified Homopolar Generator (HPG). Rather than using a separate external circuit and a spinning disk, I've combined them into a two-disk arrangement. One half of the device in fig 1a is the "disk," of a classic HPG, while the other half acts as the "external circuit." Carbon brushes connect the halves with sliding contact. Liquid metal brushes would be better.

The two halves are placed together in fig 1b. When a magnetic field is applied (vertical field in fig 1b) and the two halves are spun together as a unit, the relative motion of the metal and the magnetic field should cause a radial voltage to appear, which causes the rim of the metal assembly to aquire a positive charge, and the axis of the assembly to receive an equal negative charge. No current appears, instead the device acts like a charged capacitor as long as the rotation continues. Also, if the metal assembly is held still and the magnets are spun instead, the same radial voltage should appear and the same separation of charges should exist on the object, again with a voltage only. There is a momentary separation of charge, but no constant current.

Fig 1c shows my idea of how HPGs are able to create electric currents. If the upper and lower halves of the device are spun in opposite directions, the polarity of the radial voltage and the radial separation of charges should be opposite in each disk. Since the two halves are in sliding contact, the positive and negative regions are in electrical contact and a very large electric current should appear. This current is zero if the two halves are spun together. It is large if one half spins and the other is kept still. It is twice as large if both halves are spun in opposite directions. However, any relative rotation of the magnet, or the magnetic field, should result in equal voltages radially across both halves, and therefore should create no relative voltage between the halves, so rotating magnets should create no current. In other words, the magnetic field might spin with the magnet or it might not, but this cannot be detected by the HPG disks. The HPG doesn't care if the magnet spins. Instead, it only cares about differing rotation of the two metal parts.

If you hold one half of the metal parts still and spin the other half, you create a "classic" HPG having a spinning disk and a nonspinning "external circuit." Simply add a current meter in series with the shaft of the non-spinning half depicted above. You can even carve away most of the shell of the non-spinning half and form it into "wires". You'll end up with the "classic" HPG circuit in full.

This then shows why the rotating copper parts might apply back-action forces against the external circuit, but need not apply any forces against the permanent magnet. It explains the seeming non-reversibility of current-generating action in Faraday's homopolar experiment. It appears that there is a paradox, and that the rotation of Faraday's disk generates current, while rotation of his bar magnet does not. In reality, the only important motion is the *relative* movement between Faraday's disk and his external circuit, and the rotation of the magnet is unimportant. Of course the presence of the magnetic field is necessary to accomplish the effect and create current, but its rotation relative to the average rotation of the disk-plus-circuit assembly only creates a net radial charge separation without creating constant current.